ASP.NET Core Basics: Introduction to Big O Notation

Understanding how the performance of algorithms and data structures can impact the overall performance of an application is crucial for web developers. Learn what Big O is and how we can use it to measure the performance of our algorithms, writing more optimized and scalable code.

Big O Notation is a fundamental tool for understanding the temporal and spatial complexity of algorithms, which is essential when developing web applications and working with frameworks such as ASP.NET Core, where the manipulation of large amounts of data is common, requiring great attention to the performance of algorithms.

In this post, we will understand how to use Big O Notation to evaluate the performance of some algorithms and see five of the main time complexities in Big O Notation.

What Is Big O Notation?

According to Wikipedia, in computer science, Big O Notation is used to “classify algorithms according to how their run time or space requirements grow as the input size grows.”

In simple terms, Big O Notation is used to measure the performance or complexity of an algorithm in terms of how many resources it consumes, such as time complexity or memory space, relative to the input size.

Big O Notation describes the upper limit of the growth of an algorithm’s running time or memory space as the input size increases. It allows us to understand how the performance of an algorithm is affected by increasing problem size.

It is important to note that Big O Notation does not provide a precise measure of the absolute performance of an algorithm, but rather an overview of how performance behaves as the problem size increases, this allows developers to choose which algorithm is most indicated in a given situation, based on available resources and the requirements of the problem.

The Worst-Case Scenario

The Big O Notation establishes the time complexity for the worst case. For example, imagine that you have a list of fruits ordered by name, and you want to find the value for an apple in this list. So you choose the simple search algorithm that has the O(n) time complexity, which means that, in the worst case, all items in the list will be checked.

Suppose the apple is the first item in the list. In this case, you would not need to scan all the items. But remember that Big O considers the worst case, so even if your algorithm found the apple instantly, it still has time complexity O(n)—that is, it is considered that all items have been checked.

This is a guarantee that the simple search will never be slower than O(n) time complexity.

Growth Rates in Big O

Growth rate is a measurement that describes how a specific quantity changes over time, relative to a given variable. In computer science and algorithm analysis, growth rate often refers to how the running time (or complexity) of an algorithm increases as the input size increases.

For example, if we consider a sorting algorithm, we can observe how its time complexity increases as the number of elements to be sorted increases. The growth rate would tell us how the running time of this algorithm grows relative to the size of the input.

We can use Big O Notation to describe the growth rate of an algorithm. For example, an algorithm with complexity O(n) has a linear growth rate, which means that the time complexity increases proportionally to the size of the input, in this case, we say that the algorithm has a time complexity of O(n) where O represents the “Big O” and (n) represents the number of operations.

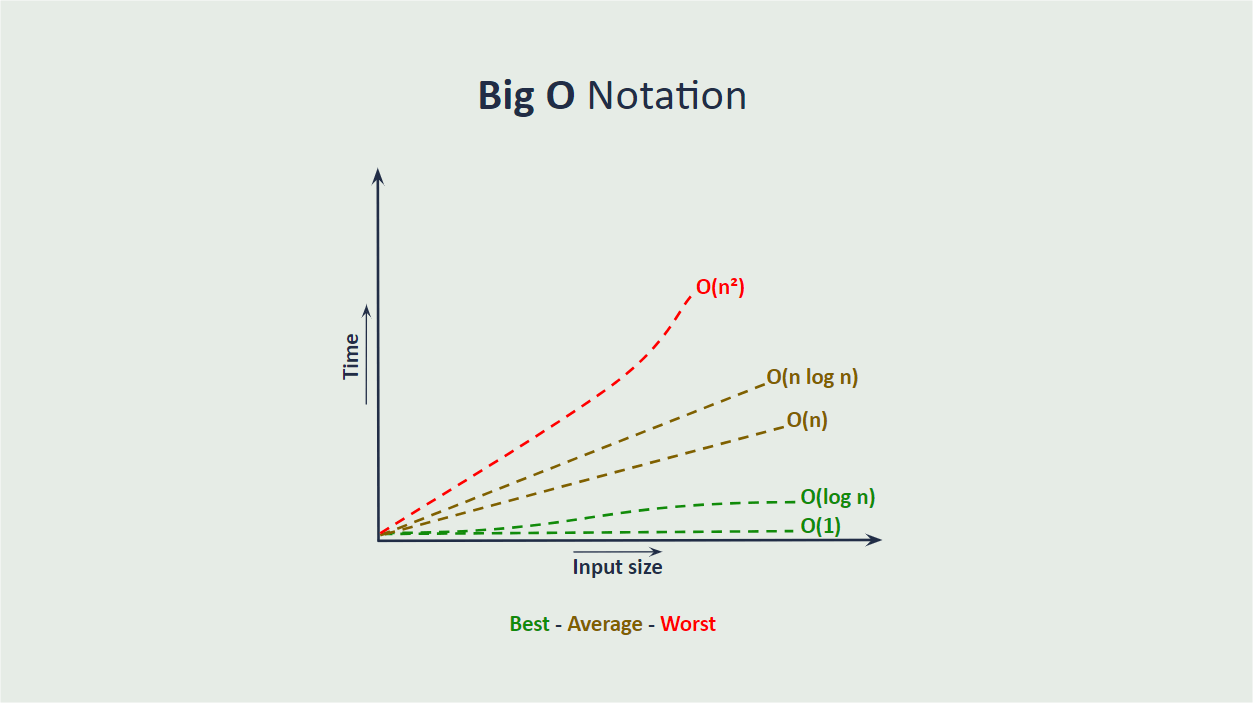
Time Complexities in Big O

There are different types of time complexity. We will talk about the five main ones, in order from fastest to slowest.

O(1) – Constant Time Complexity

O(1) complexity, also known as “constant execution time,” is highly desirable in algorithms and operations, as it means that the time required to operate does not increase as the size of the input data increases.

A very well-known example of a data structure with O(1) time complexity is arrays, where O(1) complexity is achieved by accessing an array element through its index.

This means that no matter how big the array is, the time required to access a specific element is the same as direct access to the element. It’s done in a constant step of time.

O(1) efficiency is fundamental in many algorithms and data structures, as it allows for fast and predictable operations regardless of the size of the data being manipulated. This is especially useful in situations where performance is crucial and execution time cannot be allowed to increase as data grows.

However, it is important to note that not all operations on algorithms or data structures will always be O(1). You need to consider the context and the specific operations being performed. In the example below, the search is done in an array by index, so the number of elements and the order in which they are distributed is not important. However, in examples where the search is done in the elements of the array—that is, considering the values present in the indices—other variables can be applied, resulting in a different time complexity.

To practice the examples demonstrated in the post, we will create a console application in C# and add each of the examples.

You can access the source code of the post examples here: Practicing Big O source code.

To create the application you can use the command dotnet new console -n PracticingBigONotation.

Now open the project and place the following code in the program file:

int[] array = new int[] { 10, 20, 30, 40, 50 };

int element = array[2]; 

Console.WriteLine($"Element at index 2: {element}");

The code above defines an array with some elements, then finds the value existing in the second index of the array and prints the response, where only one execution step is required, which means the function is in constant time with time complexity O(1).

In other words, whenever the search for an element occurs through the index, the search will be instantaneous, in constant time.

O(log n) – Logarithmic Time Complexity

Logarithmic time complexity, represented by O(log n), is a common characteristic of efficient algorithms in which the execution time increases logarithmically with the size of the input (n).

Logarithmic time complexity means that the running time of the algorithm increases proportionally to the logarithm of the input size.

This means that even with a substantial increase in input size, the algorithm’s running time will increase much more slowly compared to algorithms that have linear or quadratic complexity.

Algorithms with logarithmic complexity generally exploit divide-and-conquer techniques or efficient data structures to reduce the data set to be processed at each step, resulting in efficiency gains.

A good example of an algorithm with O(log n) time complexity is binary search in an ordered list. Binary search is an efficient algorithm for finding a specific element in an ordered list of elements.

Suppose you have an ordered list of elements and you want to find a specific element in that list. Binary search operates as follows:

1. Start by comparing the middle element of the list with the element you are looking for.
2. If the middle element is the same as the element you are searching for, the search is complete.
3. If the middle element is larger than the element you are looking for, you discard the top half of the list and repeat the process on the bottom half.
4. If the middle element is smaller than the element you are looking for, you discard the bottom half of the list and repeat the process on the top half.
5. Repeat this process until the element is found or until the list is reduced to zero.

The key to the efficiency of binary search is that, at each step, the list of possible elements to be considered is halved. This means that even in a large list, the number of elements to consider decreases exponentially with each iteration. As a result, the time complexity of binary search is O(log n), where n is the number of elements in the list.

To implement binary search in ASP.NET Core, we can do it as follows:

int BinarySearch(int[] arr, int target)
{
    int left = 0;
    int right = arr.Length - 1;

    while (left <= right)
    {
        int mid = left + (right - left) / 2;

        if (arr[mid] == target)
            return mid;
        if (arr[mid] > target)
            right = mid - 1;
        else
            left = mid + 1;
    }
    return -1;
}

int[] arr = { 2, 5, 6, 12, 16, 23, 38, 56, 72, 91 };
int target = 23;
int result = BinarySearch(arr, target);

if (result is not -1)
    Console.WriteLine($"Element found in position: {result}");
else
    Console.WriteLine("Element not found in array");

Now let’s analyze the code above.

The BinarySearch method starts by initializing two pointers, left and right, which represent the beginning and end indices of the array.

Then a loop is created as long as the left pointer is less than or equal to the right pointer. The mid index is calculated within the loop as the midpoint between the left and right indexes. Then it is checked whether the element in the mid position is equal to the target we are looking for. If so, we immediately return to the mid position.

If the element at the mid position is greater than the target, we update the right pointer to mid – 1, as we know that the target can only be in the left half of the array. If it is smaller, we update the left pointer to mid + 1, as the target can only be in the right half of the array.

If the loop ends and we do not find the element, we return -1 to indicate that the element is not present in the array. If we find it, then it is displayed in the console.

The binary search algorithm is efficient because, with each loop iteration, it halves the search space. This means that even in large arrays, the number of elements to consider decreases exponentially with each iteration, resulting in a logarithmic O(log n) time complexity.

O(n) – Linear Time Complexity

Linear time complexity, represented by O(n), is common in algorithms where the execution time increases linearly with the size of the input. That is, as the size of the input increases, the execution time also increases accordingly.

A common example of an algorithm with linear, O(n) time complexity is the sequential search also known as simple search, which runs on an unordered list.

To implement a sequential search, simply create an unordered list and have a target, then go through each item in the list and check at each iteration if the sought target is equal to the current element.

If the current element is equal to the target, we find the target in the list and can return the index or position where the target was found. If we go through the entire list without finding the target, we can return an indication that the target is not in the list.

The C# code below demonstrates how to implement sequential search in ASP.NET Core:

int[] unorderedArray = { 3, 1, 6, 12, 16, 23, 38, 56, 72, 83 };
int targetElement = 72;

int LinearSearch(int[] unorderedArray, int targetElement)
{
    for (int i = 0; i < unorderedArray.Length; i++)
    {
        if (unorderedArray[i] == targetElement)
        {
            return i;
        }
    }
    return -1;
}

int resultIndex = LinearSearch(unorderedArray, targetElement);

if (resultIndex != -1)
    Console.WriteLine($"Element found at index: {resultIndex}");
else
    Console.WriteLine("Element not found in the array");

Note that in the code above we pass an unordered array and an integer as the target to the LinearSearch method. Within the method, a for loop is created to traverse the array and it is checked whether the iteration element is equal to the target. If so, the index is returned; otherwise it goes to the next element. If the target is not found, the value - 1 is returned.

Algorithms with linear time complexity are generally efficient for small data sets or when there is no way to avoid inspecting every element in the input. However, on large data sets, algorithms with linear time complexity may become impractical, and more efficient algorithms may be preferred whenever possible, such as algorithms with O(log n) or O(1) time complexity for example.

O(n log n) – Log-Linear Time Complexity

The time complexity O(n log n) indicates an intermediate growth between linear (O(n)) and quadratic (O(n²)). It is common in algorithms that divide the problem into smaller parts and perform logarithmic operations on each part, followed by a linear operation that combines these parts.

Algorithms with O(n log n) time complexity are often found in sorting algorithms and in problems involving divide and conquer.

A common example of an algorithm with O(n log n) time complexity is QuickSort. QuickSort is commonly used to sort a collection of elements in ascending or descending order.

It selects a pivot element, rearranges the elements around the pivot, and then recursively sorts the two resulting partitions. The average and best-case time complexity of QuickSort is O(n log n).

To create a QuickSort in ASP.NET Core, we can do it as follows:

int[] originalArray = { 12, 4, 5, 6, 7, 3, 1, 15, 8, 9 };

Console.WriteLine("Original array:");
PrintArray(originalArray);

QuickSort(originalArray, 0, originalArray.Length - 1);

Console.WriteLine("\nOrdered array:");
PrintArray(originalArray);

void QuickSort(int[] originalArray, int low, int high)
{
    if (low < high)
    {
        int pivot = Partition(originalArray, low, high);

        QuickSort(originalArray, low, pivot - 1);
        QuickSort(originalArray, pivot + 1, high);
    }
}

int Partition(int[] originalArray, int low, int high)
{
    int pivot = originalArray[high];
    int i = low - 1;

    for (int j = low; j < high; j++)
    {
        if (originalArray[j] < pivot)
        {
            i++;
            Swap(originalArray, i, j);
        }
    }

    Swap(originalArray, i + 1, high);

    return i + 1;
}

void Swap(int[] originalArray, int i, int j)
{
    int temp = originalArray[i];
    originalArray[i] = originalArray[j];
    originalArray[j] = temp;
}

void PrintArray(int[] arr)
{
    foreach (int num in arr)
    {
        Console.Write(num + " ");
    }
    Console.WriteLine();
}

In the code above, we defined the QuickSort method, which is the main method of the algorithm. It divides the array into smaller partitions and sorts these partitions recursively.

The Partition method selects a pivot (usually the last element of the array) and rearranges the elements so that elements smaller than the pivot are on the left and elements larger than the pivot are on the right.

The Swap method is an auxiliary method that swaps the position elements in an integer array. It receives as arguments the array (originalArray) and two indices (i and j) that indicate the elements that should be replaced in the array.

To make the change, the value of the element in position i of the array is stored in a temporary variable called temp. The value of the element in position j of the array is then assigned to position i. Finally it assigns the value stored in temp (the original value of the element in position i) to position j. The PrintArray method is used to print the array on the screen.

This implementation of QuickSort sorts the array in ascending order. Still, it can be sorted according to specific needs, such as sorting in descending order or for data types other than integers.

O(n log n) time complexity is considered very efficient for different problems and is often found in algorithms that require fast sorting or efficient data manipulation.

However, it is important to remember that the efficiency of an algorithm is not only determined by its time complexity, but also by other factors such as memory usage, problem-specific requirements and detailed implementation of the algorithm.

O(n²) – Quadratic Time Complexity

O(n²) refers to the quadratic time complexity of an algorithm, where the execution time increases squarely with the input size. This means that if the input size increases, the algorithm’s running time increases by the square of that size.

This time complexity is common in algorithms that contain two nested loops, where each loop runs within an order of magnitude of n and both loops execute n times. As a result, the total execution time becomes proportional to n².

A common example with O(n²) time complexity is BubbleSort. In BubbleSort, adjacent elements are compared and swapped repeatedly until the array is sorted. This algorithm has O(n²) time complexity in the worst case, as it requires each element to be compared and possibly swapped with each other element.

To implement BubbleSort in ASP.NET Core we can use the following:

int[] originalArray = { 64, 34, 25, 12, 22, 11, 90 };
        
Console.WriteLine("Original array:");
PrintArray(originalArray);

BubbleSort(originalArray);

Console.WriteLine("\nOrdered array:");
PrintArray(originalArray);

static void BubbleSort(int[] arr)
{
    int n = arr.Length;
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n - i - 1; j++)
        {
            if (arr[j] > arr[j + 1])
            {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

static void PrintArray(int[] arr)
{
    foreach (int num in arr)
    {
        Console.Write(num + " ");
    }
    Console.WriteLine();
}

In the code above, we define an unordered array, and then pass it to the BubbleSort method. In this method, we define the variable n that receives the array’s length. This lets us know how many elements there are in the array.

Then we create the first loop for (int i = 0; i < n - 1; i++), which is the outer loop of BubbleSort. It traverses the array from left to right and is responsible for controlling the number of iterations. The loop goes until the penultimate element of the array, because in the last iteration, the last element will already be in the correct place.

Then we define the second loop for (int j = 0; j < n - i - 1; j++), which is the internal loop of BubbleSort. It also traverses the array from left to right, but the number of iterations decreases with each pass through the outer loop (i). This is because, with each iteration of the outer loop, the largest element is already in the correct position at the end of the array.

Using the condition if (arr[j] > arr[j + 1]), we check whether the current element (arr[j]) is greater than the next element (arr[j + 1]). If so, it means they are out of order and need to be changed.

So, we changed the elements using the code int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp;. First, the value of the current element (arr[j]) is stored in a temporary variable (temp). Then, the value of the next element (arr[j + 1]) is assigned to the current element.

Finally, the value stored in temp (the original value of the current element) is assigned to the next element. This exchanges the elements.

It is important to note that algorithms like BubbleSort are simple to understand and implement, but can be inefficient for large data sets due to their quadratic complexity.

In scenarios where efficiency is crucial, it is preferable to use algorithms with lower time complexity, such as O(n log n) or O(n), to avoid excessive execution time.

Conclusion

It is important that ASP.NET Core developers and in general learn about Big O Notation, because through it we can understand the temporal and spatial complexity of the algorithms we develop, increasing accuracy when choosing the right algorithm for the problem we are solving.

In this post, we saw what Big O Notation is and analyzed the five main time complexities, implementing a practical example of each of them.

There are also other time complexities and other details that were not covered in this post, as it aims to provide an introduction to Big O and some of the main examples.

So, when dealing with a problem, consider using Big O Notation to evaluate the best option to choose.